数量关系(二核心题型解题方法)【行测】-湛江公务员培训
二、核心题型解题方法
▲工程问题
(1)基础知识
1. 工作量 = 工作效率 × 工作时间
2. 工作效率 = 工作量 ÷ 工作时间
(2)解题思路:
1. 条件只给岀时间的具体值: 通过给总量赋值, 一般将总量设为时间的公倍数,从而计 算出给出条件的效率。
2. 条件中不仅有时间,而且有关于效率的比例关系, 通常给效率赋值,通过公式计算出 工作总量。
3. 题目中有效率、时间、总量三个中的任意两个的具体值,则代入公式计算出第三个即可。
随笔练习
1.(2017 广东 ) 现有一批零件,甲师傅单独加工需要 4 小时,乙师傅单独加工需要 6 小时。 两人一起加工这批零件的 50% 需要多少个小时 ?( )
A.0.6 B.1 C.1.2 D.1.5
※【答案】C。解析:题中给出 4 和 6 两个完工时间,因此赋值工程总量为 4 和 6 的最 小公倍数 12, 甲的效率为:12÷4=3,乙的效率为: 12÷6=2,一起合作加工零件的 50% 需 要的时间为:12×50%÷(3+2)=1.2 小时。故正确答案为 C。
2.(2016 国考 ) 某浇水装置可根据天气阴晴调节浇水量, 晴天浇水量为阴雨天的 25 倍。 灌满该装置的水箱后,在连续晴天的情况下可为植物自动浇水 18 天。小李 6 月 1 日 0: 00 灌满水箱后,7 月 1 日 0:00 正好用完。问 6 月有多少个阴雨天 ?
A.10 B.16 C.18 D.20
※【答案】 D。解析:由题目所给出的晴天浇水量与阴雨天浇水量之比,可假设晴天浇 水量为 5,阴雨天浇水量为 2,则可得水箱总容量为 5×18=90。已知 6 月整月共有 30 天, 设阴雨天数为 a,晴天数为 (30-a),则 5(30-a)+2a=90,解得 a=20。故正确答案为 D。
▲行程问题
(一)基础知识:
基本公式:路程 = 速度 × 时间
相遇问题:路程和 =( 大速度 + 小速度 )× 时间
追及问题:路程差 =( 大速度-小速度 )× 时间
顺水行船:路程 =( 船速 + 水速 )× 时间
逆水行船:路程 =( 船速 - 水速 )× 时间
火车过桥(隧道): 路程 = 火车车身长度 + 桥长(隧道长度) = 火车速度 × 过桥速度(过 隧道速度)
(2)解题思路:
根据题干先判断出题型, 尽量能画出简易图,根据各个量之间的关系代入上述对应的公 式即可。
(三)补充知识:
①时间一定,路程和速度成正比;
②路程一定,速度和时间成反比;
③速度一定,路程和时间成正比。
④当行程中某一个量为定值,且出现比例时,可以考虑用比例求解。
随笔练习
1.(2018 国考 ) 一辆汽车第一天行驶了 5 个小时, 第二天行驶了 600 公里, 第三天比第 一天少行驶 200 公里, 三天共行驶了 18 个小时。已知第一天的平均速度与三天全程的平均 速度相同,问三天共行驶了多少公里 ?( )
A.800 B.900 C.1000 D.1100
※【答案】 B。解析:本题属于基本行程问题,利用基本公式。设第一天的平均速度为 ν,第一天路程为 5v,第三天路程为 5v-200。由全程平均速度与第一天相同,可得方程: 5v+600+5y-200=18ν,解得 v=50,则三天共行驶 18×50=900 公里。故正确答案为 B。
2.(2018 联考 ) 甲、乙、丙、丁四人同时同地出发,绕一椭圆形环湖栈道行走。甲顺时针行走, 其余三人逆时针行走。已知乙的行走速度为 60 米 / 分钟,丙的速度为 48 米 / 分钟。甲在出发 6、 7、8 分钟时分别与乙、丙、丁三人相遇,求丁的行走速度是多少 ?( )
A.31 米 / 分钟 B.36 米 / 分钟
C.39 米 / 分钟 D.42 米 / 分钟
※【答案】C。解析:由题意可知,甲与乙相遇,甲与丙相遇均为两人合走完一个环湖的全程。 根据总路程相等,可得方程 (v 甲 +60)×6=(v 甲 +48)×7,解方程得 v 甲 =24 米 / 分钟。同理, 甲与乙相遇,甲与丁相遇时的路程也相等,(24+60)×6=(24+V 丁 )×8,解得 v 丁 39 米 / 分钟。 故正确答案为 C。
3.(2017 山东 ) 有 A、B 两家工厂分别建在河流的上游和下游,甲、乙两船分别从 A、B 港口出发前往两地中间的 C 港口。C 港与 A 厂的距离比其与 B 厂的距离远 10 公里。乙船出 发后经过 4 小时到达 C 港,甲船在乙船出发后 1 小时出发,正好与乙船同时到达。已知两船 在静水中的速度都是 32 公里 / 小时,问河水流速是多少公里 / 小时 ?( )
A.4 B.5 C.6 D.7
※【答案】C。解析:由题意可得, 甲船比乙船多行驶 10 公里,甲船用时 4-1=3 小时。 设河水流速为 ν 公里 / 小时,则有 3×(32+v)-4×(32-v)=10,解得 v=6。故正确答案为 C。
▲经济利润问题
(一)基础知识
1. 利润 = 售价 - 进价
2. 利润率 = 利润 ÷ 进价 =( 售价 - 进价 )÷ 进价
3. 售价 = 进价 ×(1+ 利润率 )
(二)解题思路
根据上述公式列方程。若题干中未出现具体单位,可以利用赋值法求解。在解题中,可 以利用数字特性快速求解。
随笔练习
1.(2018 江西 ) 小李四年前投资的一套商品房价格上涨了 50%,由于担心房价下跌,将 该商品房按市价的 9 折出售, 扣除成交价 5% 的相关交易费用后, 比买进时赚了 56.5 万元。 那么,小李买进该商品房时花了多少万元 ?( )
A.200 B.250 C.300 D.350
※【答案】A。解析:设买进该商品房时成本为 x 万元,则现在市价为 1.5x 万元,实际 售价为 1.5x×0.9=1.35x 万元。利润:(1-5%)×135x-x=56.5,解得 x=200。故正确答案为 A。
2.(2018 国考 ) 枣园每年产枣 2500 公斤, 每公斤固定盈利 18 元。为了提高土地利用率, 现决定明年在枣树下种植紫薯 ( 产量最大为 10000 公斤 ),每公斤固定盈利 3 元。当紫薯产 量大于 400 公斤时,其产量每增加 n 公斤将导致枣的产量下降 0.2n 公斤。问该枣园明年最 多可能盈利多少元 ?( )
A.46176 B.46200 C.46260
D.46380
※【答案】 B。解析: 当紫薯产量大于 400 公斤时,每增加 n 公斤将导致枣的产量下降 0.2n 公斤。假设紫薯的产量为 (400+n) 公斤,则此时枣的产量为 (2500-0.2n) 公斤。则总盈 利为 18×(2500-0.2n)+3×(400+n)=(46200-0.6n) 元,要让总盈利最大,则 n 取 0,此时总盈 利为 46200 元。故正确答案为 B。
▲几何问题
(一)基础知识
1. 基本公式


2. 常用三角函数

3. 三角形常用知识点
(1)两边之和大于第三边,两边之差小于第三边。
(2)三角形内角和为 180°。
(3)勾股定理: a2 + b2 = c2 (常用勾股数:3、4、5;6、8、10;5、12、13)
(二)解题思路
1. 规则图形,按照相对应的公式列方程或直接计算;
2. 不规则图形,通过割、补、平移等方法转化成规则图形,再按照相对应的公式列方程 或直接计算。
随笔练习
1.(2015 国考 ) 某学校准备重新粉刷升国旗的旗台,该旗台由两个正方体上 下叠加而成,边长分别为 1 米和 2 米,问需要粉刷的面积为:( )
A.30 平方米 B.29 平方米
C.26 平方米 D.24 平方米
※【答案】 D。解析:小正方体每个面的面积为 12=1m2,大正方体每个面的面积为 22=4m2,两个正方体的总面积为 6×1+6×4=30m2,其中重合部分为两个小正方体的面, 面积为 2×1=2m2,而大正方体作为旗台,其底面不用粉刷,故需要粉刷的面积为 30-2- 4=24m2。故正确答案为 D。
2.(2015 国考 ) 现要在一块长 25 公里、宽 8 公里的长方形区域内设置哨塔,
每个哨塔的监视半径为 5 公里。如果要求整个区域内的每个角落都能被监视到,则至少 需要设置多少个哨塔 ?( )
A.7 B.6 C.5 D.4
※【答案】C。解析:如下图所示:

根据直角三角形勾股定理有 52-42=32,则每个圆形可覆盖一个宽为 3×2=6 公里的长方
形。要达到完全覆盖,故需要 ≈ 4.17 个,至少 5 个。故正确答案为 C。
≈ 4.17 个,至少 5 个。故正确答案为 C。
3.(2018 国考 ) 一艘非法渔船作业时发现其正右方有海上执法船,于是沿下图所示方向 左转 30°后, 立即以 15 节 (1 节 =1 海里 / 小时 ) 的速度逃跑, 同时执法船沿某一直线方向匀 速追赶,并正好在某一点追上。已知渔船在被追上前逃跑的距离刚好与其发现执法船时与执 法船的距离相同,问执法船的速度为多少节 ?

※【答案】 D。解析:

根据题意可知,非法渔船和执法船的行驶路线为上图所示,非法渔船在 A 点被追 上。由于非法渔船的逃跑距离和发现执法船时其与执法船的距离相同,假设距离为 a, 即 OA=OB=a; 渔 船 左 转 30 °, 即 ∠ AOB=120 °。 又 因 为 △ AOB 为等 腰三 角 形, 故 ∠ OBA= ∠ OAB=30 °。 过 点 O 作 OC 垂 直 AB 于 点 C, 根 据 △ OCB 为 直 角 三 角 形, 且

▲排列组合及概率问题
(一)基础知识
加法原理:分类用加法
乘法原理:分步用乘法
排列:与顺序有关
组合:与顺序无关

(二)特殊方法
当题目中要求某些主体必须排在一起时,考虑捆绑法。 当题目中要求某些主体不能相邻时,考虑插空法。
相同的物品分给多个主体时,要求每个主体至少分 N 个,就可以考虑插板法。先给每个 主体少分一个 ( 即 N-1 个 ),剩下的物品必须给每个主体至少再分 1 个才能满足要求,此时 将剩下的物品插板分堆即可, 插板数量 = 主体个数 -1。
当题目中要求不能一一对应时, 比如: N 把钥匙对应 N 个锁, 要求每个锁和一把不能打
开它的钥匙放进一个信封,这就是错位排列。错位排列用 D,表示, Dn 就表示 N 个数字的 错位排列。
D1=0,D2=1,D3=2,D4=9,D5=44。
(三)解题思路
当题干中有特殊要求时,按照对应的特殊方法求解。没有特殊要求的,按照基础知识列 式求解即可。
随笔练习
1.(2014 国考 ) 一次会议某单位邀请了 10 名专家, 该单位预定了 10 个房间, 其中一层 5 间、二层 5 间。已知邀请专家中 4 人要求住二层, 3 人要求住一层,其余 3 人住任一层均可, 那么要满足他们的住房要求且每人 1 间,有多少种不同的安排方案 ?( )
A.43200 B.7200 C.450 D.75
※【答案】A。解析:先安排有要求的专家,再安排没有要求的专家,即分步进行安排即可。
首先安排需要住二层的人, 从 5 间二层房间中选出 4 间, 安排 4 名专家的方法有 A5种;
再安排需要住一层的人,从 5 间一层房间中选出 3 间,安排 3 名专家的方法有 A5种;最后
安排剩下的 3 人,无任何要求,安排方法有 A3种。分步用乘法,安排方法共有 A5× A5× A3
=43200 种。故正确答案为 A。
2.(2017 国考 ) 某集团企业 5 个分公司分别派出 1 人去集团总部参加培训,
培训后再将 5 人随机分配到这 5 个分公司, 每个分公司只分配 1 人。问 5 个参加培训的 人中,有且仅有 1 人在培训后返回原分公司的概率:( )
A. 低于 20% B. 在 20%~30% 之间
C. 在 30%~35% 之间 D. 大于 35%
※【 答 案 】 D。 解 析:5 个 人 任 意 分 配 到 5 个 分 公 司 的 总 情 况 数 为 A5
=5×4×3×2×1=120;满足只有 1 人培训后返回原分公司的情况数为:5×D4=45( 先在 5 人中
任选 1 人返回原分公司,共有C5 =5 种选择;再将剩下 4 人错位排列, D4=9)。则所求概率
满足要求的情况数 45 3


 = 总的情况数 = 120 = 8 =37.5%>35%,故正确答案为 D。
= 总的情况数 = 120 = 8 =37.5%>35%,故正确答案为 D。
3.(2016 国考 ) 为加强机关文化建设,某市直属机关在系统内举办演讲比赛。3 个部门 分别派出 3、2、4 名选手参加比赛,要求每个部门的参赛选手比赛顺序必须相连,问不同参 赛顺序的种数在以下哪个范围之内 ?( )
A. 小于 1000 B.1000 ~ 5000
C.5001 ~ 20000 D. 大于 20000
※【答案】 B。解析:3 个部门分别派出 3、2、4 名选手参加比赛,要求每个部门的 参赛选手比赛顺序必须相连。可先对每个部门内部的选手进行全排列,然后将 3 个部门的

▲溶液问题
(一)基本公式

溶质的质量 = 溶液的质量 × 浓度
(二)溶液混合问题——十字交叉法
1. 溶液混合问题,指两种不同浓度、不同质量的溶液混合在一起, 形成新的浓度。这是 溶液问题中基本题型, 常用解法为十字交叉法。
步骤为:
①写两个部分量的浓度;
②写整体浓度;
③十字交叉作差(大数-小数);
④写差值最简比;
⑤最简比对应两部分溶液的质量之比。
2. 十字相乘法使用时要注意几点:
①用来解决两者之间的比例关系问题。
②得出的比例关系是基数的比例关系。
③总均值放中央,对角线,大数减小数,结果放对角线上。
(三)十字交叉模型

1. 三组计算关系:
第一列和第二列交叉作差得到第三列(大数减小数)。 第三列、第四列和第五列的比值相等。
第一列的差等于第三列的和。
2. 最简比(实际量之比)为比值的分母之比。
随笔练习
1. 要将浓度分别为 20% 和 5% 的 A、B 两种食盐水混合配成浓度为 15% 的食盐水 900 克。 问 5% 的食盐水需要多少克?( )
A.250 B.285
C.300 D.325
※【答案】C。解析: 方法一:方程法
A 食盐水的记为 A 溶液 B 食盐水记为 B 溶液

溶液的质量 ×10%。设 A、B 两种溶液的质量分别为 900-x、x 克,根据等量关系可得方程 5% (900-x)=10%x,解得 x=300。
方法二:十字交叉法
将相应数据填入括号内


2. 甲容器中有浓度 4% 的盐水 150 克,乙容器中有某种浓度的盐水若干,若从乙容器中 取出 450 克盐水放入甲中混合成浓度为 10% 的盐水,问乙容器中盐水的浓度是多少?( )
A.11% B.12%
C.14% D.16%
※【答案】 B。解析:此题为溶液混合问题,设乙容器中盐水的浓度为 x%,应用十字交 叉法如下:
甲:4% x%-10% 150
↘ ↙ 10%
↙ ↘
乙:x% 10%-4% 450
因此, 有 
 , 解得 x%=12%, 故正确答案为 B。
, 解得 x%=12%, 故正确答案为 B。
▲和定最值问题
(一)基础知识
如何来判断一个题目是否属于和定最值问题,我们需要按以下两个条件去排除:
1. 几个数的和一定;
2. 问题是求其中某个量的最大值或者最小值。
(二)题型特点
题干或问法中出现“最大或最小、最多或最少、至多或至少。”等,我们首先要考虑是 和定值问题。和定最值:多个数的和一定,求其中某个量的最大或最小值的问题。
(三)解题原则
1. 求某个量的最大值,让其余量尽可能小,从最小开始分析 。
2. 求某个量的最小值,让其余量尽可能大,从最大开始分析。
随笔练习
1. 要把 21 棵桃树栽到街心公园里 5 处面积不同的草坪上,如果要求每块草坪必须有树 且所栽棵数要依据面积大小各不相同,面积最大的草坪最多栽多少棵桃树? ( )
A.7 B.8
C.10 D.11
※【答案】 D。解析:存在“和”。“和”为 21。所求为最大量的最大值。要使面积最大的草 坪栽种的桃树最多,则其他草坪栽种的桃树应尽可能的少。设面积最大的草坪栽了 x 棵,其 他四个草坪栽种的桃树棵数分别为 1、2、3、4,则 x+4+3+2+1=21 棵,解得 x=11。
2. 期末考试中前六名学生成绩的平均分是 92.5 分,且 6 人的成绩是互不相同的整数, 最高分是 99 分,则第三名至少得多少分?
A.91 B.93
C.96 D.97
※【答案】A。解析:存在“和”。“和”为 92.5×6=555。所求为第三名的最小值。要使第 三名的分数尽可能低,则其他人分数应尽量高。第一、二名最高可为 99、98 分,设第三名 为 x 分,则第四、第五、第六依次为 x-1、x-2、x-3 分,99+98+x+x-1+x-2+x-3=555,解得 x=91 分。
3.6 名同学参加一次百分制考试, 已知 6 人的分数是互不相同的整数。若 6 名同学的总 分是 513 分,求分数最低的最多得了多少分?( )
A.83 B.84
C.85 D.86
※【答案】A。解析:存在“和”。“和”为 513。所求为最小量的最大值。要想分数最低的 同学得分最多,则其他同学的得分应尽可能的少。设分数最低的同学得了 x 分,其他 5 个同 学的得分分别为 x+1、x+2、x+3、x+4、x+5, 则 x+x+1+x+2+x+3+x+4+x+5=513 分, 解 得 x=83。
▲容斥问题
(一)两者容斥
如果被计数的事物有 A、B 两类,那么,先把 A、B 两个集合的元素个数相加,发现即 是 A 类又是 B 类的部分重复计算了一次,所以要减去。如下图所示。

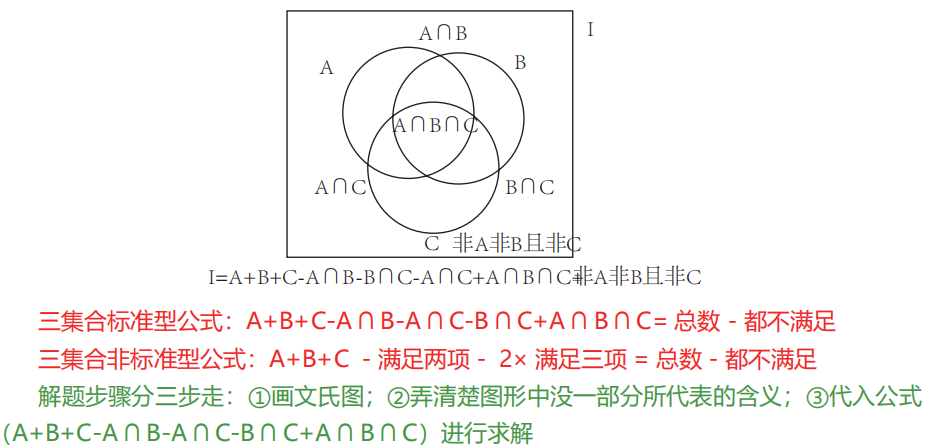
(三)容斥极值
公式:(A ∩ B)min=A+B-1
推广:(A ∩ B ∩ C)min=A+B+C-21
随笔练习
1. 某公司组织歌舞比赛, 共 68 人参赛。其中, 参加舞蹈比赛的有 12 人, 参加歌唱比 赛的有 18 人,45 人什么比赛都没有参加。问同时参加歌舞比赛的有多少人? ( )
A.7 B.8
C.9 D.10
※【答案】A。解析:总人数 = 参加舞蹈比赛人数 + 参加歌唱比赛人数 - 两项比赛都参 加人数 + 两项比赛都未参加人数。所以两项比赛都参加的人数为 12+18-(68-45)=7 人。
2. 某市对 52 种建筑防水卷材产品进行质量抽检, 其中有 8 种产品的低温柔度不合格, 10 种产品的可溶物含量不达标, 9 种产品的接缝剪切性能不合格, 同时两项不合格的有 7 种, 有 1 种产品这三项都不合格。则三项全部合格的建筑防水卷材产品有多少种? ( )
A.34 B.35
C.36 D.37
※【答案】A。解析:在将低温柔度不合格、可溶物含量不达标、接缝剪切性能不合格 的产品数相加时,两项同时不合格的产品数被计算了两次,需减掉一次;三项同时不合格的 产品数被计算了三次,需减掉两次。设三项全合格的建筑防水卷材产品有 x 种,根据容斥原 理可得,8+10+9-7-2×1+x=52,解得 x=34。
3. 阅览室有 100 本杂志。小赵借阅过其中 75 本, 小王借阅过 70 本, 小刘借阅过 60 本, 则三人共同借阅过的杂志最少有多少本?( )
A.5 B.10
C.15 D.30
※【答案】A。解析:本题出现了三个概念,分别是小赵借阅、小刘借阅、小王借阅, 概念间存在交叉关系。根据三个集合交集最小值的公式,三人都借阅的至少有 75+70+60- 2×100=5 本。
▲计算问题
(一)等差数列
1. 基础知识
等差数列是指从第二项起, 每一项与它的前一项的差等于同一个常数。例如: 1, 3, 5, 7,9……。数列的第一项叫做首项 a1 表示,数列的最后一项叫做末项用 an 表示。
相邻两项的差值叫做共差 d 表示。前项和用 Sn 表示。
2. 基本公式

(二)周期循环
解题关键:寻找最小循环周期。
(1)找周期: 找准周期的起点和终点,确定总数
(2)算余数: 总数 ÷ 每个周期的个数 = 周期数量……余数(n)
(3)做等价: 余数 n 就等价于该周期的第 n 项(余几数几)
(三)整除
1. 核心
通过题干中所给的信息,判断结果应具备的整除特性,从而排除错误选项
2. 应用环境
题干文字描述中出现“整除、每、平均、倍数”等字眼时能用利用整除解题题干中出现分数、 百分数、比例等数据时能够利用整除解题
随笔练习
1. 某剧院共 25 排座位,后一排均比前一排多 2 个座位,已知最后一排有 80 个座位, 问这个剧院一共有多少个座位?( )
A.1200 B.1300
C.1400 D.1500

※【答案】A。解析: 一个完整的循环是“3 本小说 +4 本教材 +5 本工具书 +7 本科技书” 共 19 本书,所以最小循环周期为 19。136÷19=7……3,所以有 7 个完整的循环周期。还多 3 本, 正好多 3 本小说,最后一本为小说。
3. 学校有足球和篮球的数量比为 8 ∶ 7,先买进若干个足球,这时足球与篮球的比变为 3 ∶ 2,接着又买进一些篮球,这时足球与篮球数量比为 7 ∶ 6。已知买进的足球比买进的篮 球多 3 个,原来有足球多少个?( )
A.48 B.42
C.36 D.30
※【答案】A。解析:由题意可知,原来足球的个数能被 8 整除。只有 A 项能够被 8 整除。







